목차
- 파라독스란?
- 고전적인 수학 파라독스
- 현대의 흥미로운 파라독스
- 확률과 통계의 파라독스
- 결론
들어가며
여러분, 안녕하세요! 오늘은 여러분과 함께 수학에서 가장 흥미진진한 주제인 '파라독스'에 대해 이야기해보려고 합니다.
"도대체 어떻게 이런 일이 가능할까요?"라는 질문으로 시작하는 신비로운 수학의 세계로 함께 떠나볼까요?
1. 제논의 파라독스: "움직임은 불가능하다?"
Q: 여러분, 교실 앞까지 걸어올 수 있나요?
"당연히 걸어갈 수 있죠!"라고 대답하시겠지만, 잠깐만요!
다음 과정을 생각해봅시다:
- 교실 앞까지 가려면 먼저 절반의 거리를 가야 해요
- 남은 거리의 절반을 또 가야 하고
- 또다시 남은 거리의 절반을...
- 이런 식으로 무한히 계속됩니다
왜 이것이 파라독스일까요?
- 수학적으로는 무한히 많은 단계를 거쳐야 함
- 각 단계는 0보다 큰 시간이 필요
- 따라서 이론상 목적지에 도달하는 것은 불가능!
하지만 우리는 실제로 걸어갈 수 있죠? 이것이 바로 파라독스입니다!
해결방법
이 파라독스는 무한급수의 개념으로 설명할 수 있어요:
- 1/2 + 1/4 + 1/8 + 1/16 + ... = 1
- 무한히 더해도 유한한 값이 나올 수 있다는 것!
2. 무한호텔 파라독스: "만실인데 방이 남는다고요?"
Q: 무한개의 방이 있는 호텔이 만실인데, 새로운 손님이 왔다면?
"방이 없으니 받을 수 없죠!"라고 생각하시나요?
해결방법을 함께 생각해봅시다:
- 현재 투숙객 상황
- 1번 방: A님
- 2번 방: B님
- 3번 방: C님
- ...무한히 계속
- 모든 손님을 한 방씩 뒤로 이동
- A님 → 2번 방
- B님 → 3번 방
- C님 → 4번 방
- ...
짜잔! 1번 방이 비었습니다!
더 놀라운 것은?
무한명의 새로운 손님이 와도 수용할 수 있어요!
- 기존 손님: 원래 방 번호 × 2로 이동
- 새로운 손님: 홀수 번호 방에 배정
3. 몬티 홀 문제: "직관을 믿지 마세요!"
Q: 세 개의 문 중 하나를 선택하면 자동차를 받을 수 있습니다. 선택을 바꿔야 할까요?
상황 설정:
- 세 개의 문 중 하나에 자동차, 나머지는 염소
- 참가자가 한 문을 선택
- 진행자가 염소가 있는 다른 문을 열어줌
- 선택을 바꿀 기회를 줌
대부분의 사람들이 하는 생각
"어차피 두 개 중 하나니까 확률은 1/2이죠!"
실제 확률
- 처음 선택을 유지: 1/3
- 선택을 바꾸면: 2/3
왜 이럴까요?
자세히 분석해보면:
- 처음 선택 시 자동차를 고를 확률: 1/3
- 염소를 고를 확률: 2/3
- 진행자가 염소를 보여주면?
- 처음에 자동차를 골랐다면 → 바꾸면 염소
- 처음에 염소를 골랐다면 → 바꾸면 자동차
4. 생일 파라독스: "23명이면 충분하다고요?"
Q: 한 교실에 학생이 23명 있다면, 같은 생일자가 있을 확률은 얼마일까요?
대부분 "매우 낮을 것"이라 생각하지만... 실제로는 50.7%나 됩니다!
계산 과정
- 모두 다른 생일일 확률 계산
- 첫 번째 사람: 365/365
- 두 번째 사람: 364/365
- 세 번째 사람: 363/365
- ...
- 같은 생일이 있을 확률
- 1 - (다른 생일일 확률)
- 약 0.507 = 50.7%
5. 심슨의 파라독스: "전체와 부분이 다르다고요?"
Q: A병원이 B병원보다 모든 질병의 치료율이 높은데, 전체 치료율은 낮다?
예시 데이터:
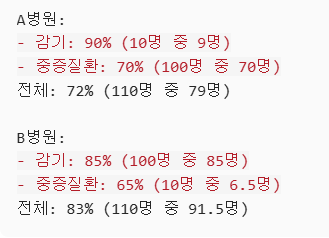
왜 이런 현상이 발생할까요?
- 환자 구성비의 차이
- 가중평균의 특성
- 표본 크기의 영향
마치며
파라독스는 우리의 직관을 시험하고, 더 깊은 사고를 요구합니다. 하지만 이를 통해 우리는:
- 비판적 사고력 향상
- 수학적 직관 발달
- 논리적 사고 능력 개발
이러한 것들을 배울 수 있죠!
학습 포인트 정리
- 파라독스는 오류가 아닌 사고의 확장
- 직관을 넘어선 논리적 사고의 중요성
- 수학적 증명의 필요성
- 확률과 통계의 올바른 이해
추천 학습 방법
- 각 파라독스를 친구들과 토론해보기
- 실제 데이터로 계산해보기
- 일상생활에서 비슷한 사례 찾아보기
- 수학적 증명 과정 이해하기
'수학' 카테고리의 다른 글
| 삼각비와 삼각함수의 탄생: 역사적 배경과 실생활에서의 유용한 활용법 (0) | 2025.01.31 |
|---|---|
| 로그(log)의 탄생: 배경, 종류, 그리고 실생활에서의 놀라운 활용법 (0) | 2025.01.30 |
| 금융 수학의 기초: 투자 의사결정을 위한 필수 개념과 활용법 (0) | 2025.01.27 |
| 인공지능 혁신의 열쇠: 수학이 이끄는 AI 기술의 비밀 (0) | 2025.01.26 |
| [확률과 통계] 통계적 추정: 설문조사를 활용한 데이터 분석의 원리와 응용 (0) | 2025.01.26 |